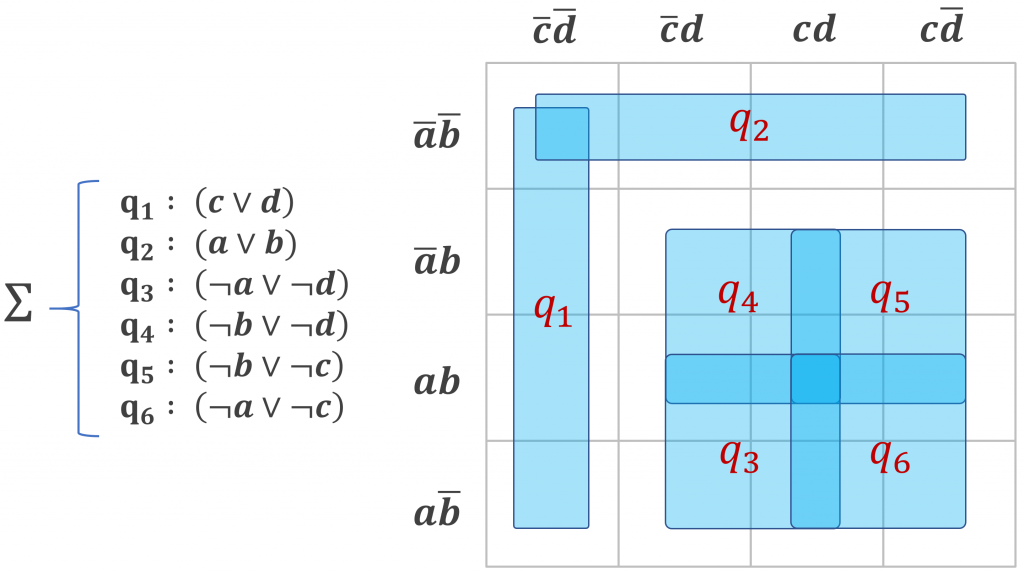
Raisonner c’est paver. C’est en tout cas la vision que je défends dans une note de recherche en anglais téléchargeable ici. L’idée est de représenter l’espace d’interprétation des variables d’une formule propositionnelle par un hypercube, et chaque clause de cette formule comme une dalle hypercubique couvrant une partie de cet espace. Déterminer si la formule est cohérente revient alors à rechercher s’il existe un sommet de l’hypercube non recouvert par une clause.
Je présente dans ce billet une idée qui est décrite en anglais dans cette note. Elle consiste à exploiter des séquences d’hypothèses et de déductions pour produire des clauses qui sont conséquences logiques de celles ayant servi à réaliser les déductions, comme le font les solveurs CDCL, mais avec une approche différente, permettant de produire d’autres clauses.
Par exemple, considérons cette séquence contradictoire d’hypothèses et de déductions qui pourrait être produite par un solveur SAT de type CDCL ou même DPLL. Je propose d’appeler une telle séquence AUP-séquence contradictoire (AUP pour Assumption and Unitary Propagation).
La Résolution générale est le fondement des solveurs SAT complets actuels, de type CDCL, de ceux de la générations précédente, de type DPLL, et de ceux de première génération, qui l’utilisaient de manière plus directe.
Étant donnée une formule CNF 
, Produire une réfutation de de taille minimale en terme de nombre de déductions est intéressant à au moins deux titres : (1) la taille d’une telle réfutation donne une information sur la difficulté intrinsèque de pour la Résolution, et en particulier donne une borne inférieure de l’effort de calcul nécessaire pour réfuter , et (2) toute réfutation est une explication de l’incohérence d’une formule, et plus cette explication est courte, plus elle est, d’une certaine façon, pertinente.