SAT est un problème de pavage d’hypercube

Raisonner c’est paver. C’est en tout cas la vision que je défends dans une note de recherche en anglais téléchargeable ici. L’idée est de représenter l’espace d’interprétation des variables d’une formule propositionnelle par un hypercube, et chaque clause de cette formule comme une dalle hypercubique couvrant une partie de cet espace. Déterminer si la formule est cohérente revient alors à rechercher s’il existe un sommet de l’hypercube non recouvert par une clause.

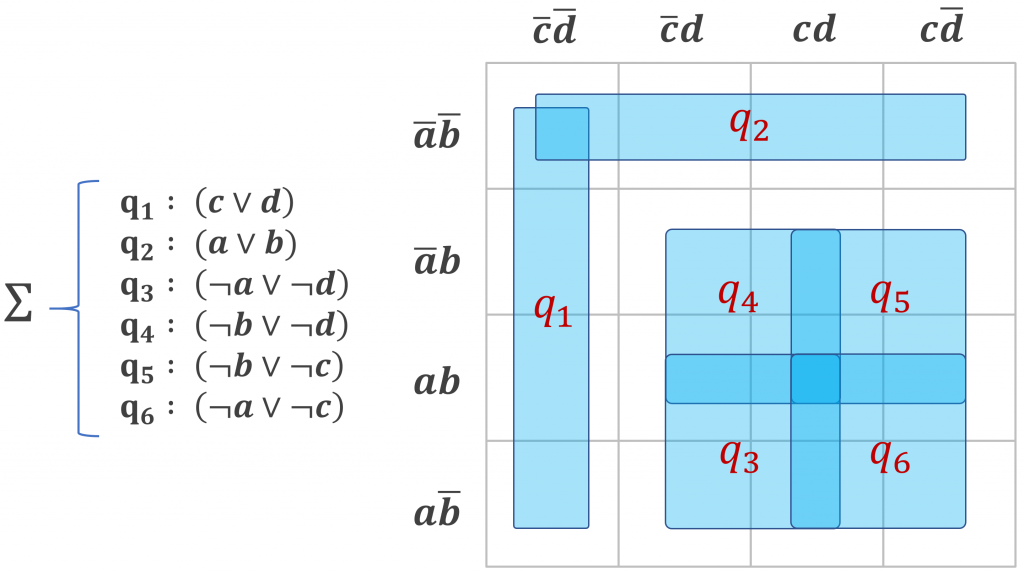
Résolution et pavage

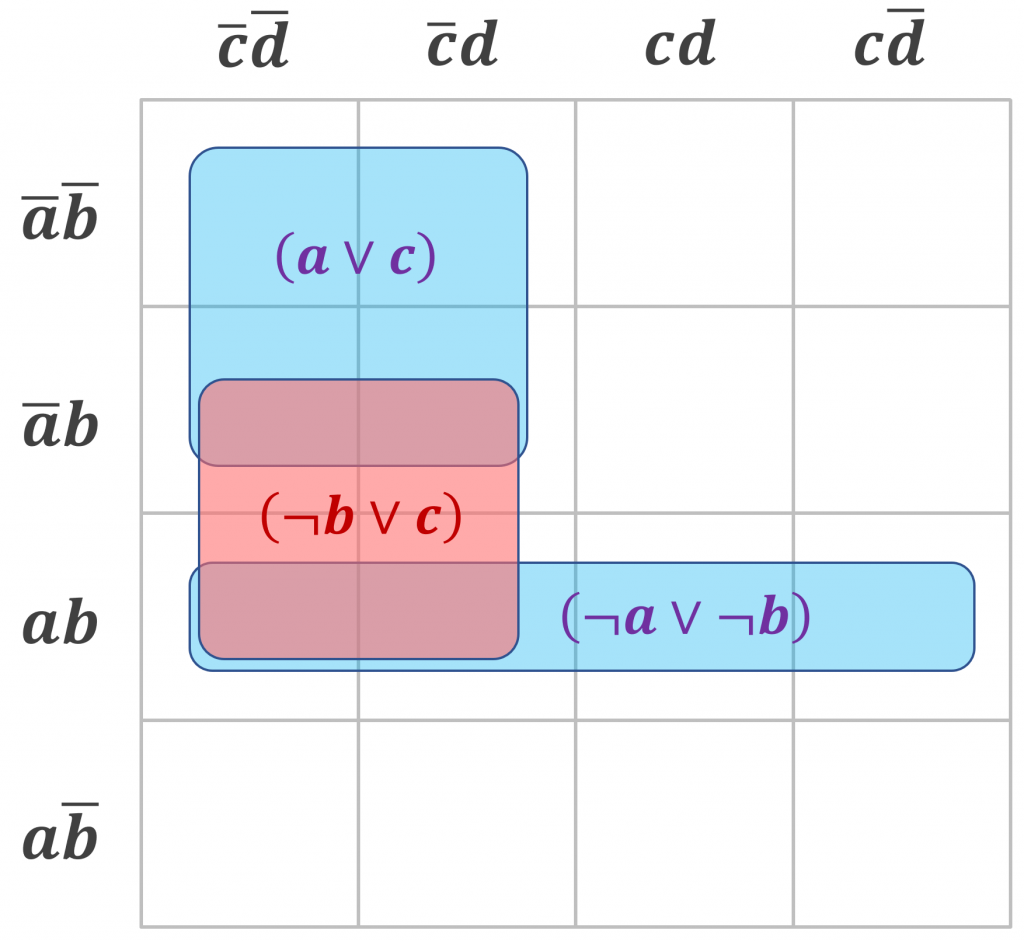
La plupart des solveurs SAT complets actuel (et anciens) sont basés sur une règle d’inférence appelée Résolution, qui se décrit facilement comme la production d’une dalle à partir de deux dalles contigües. La dalle résolvante est la plus grande dalle hypercubique complètement couverte par les deux prémisses. Voici un exemple.

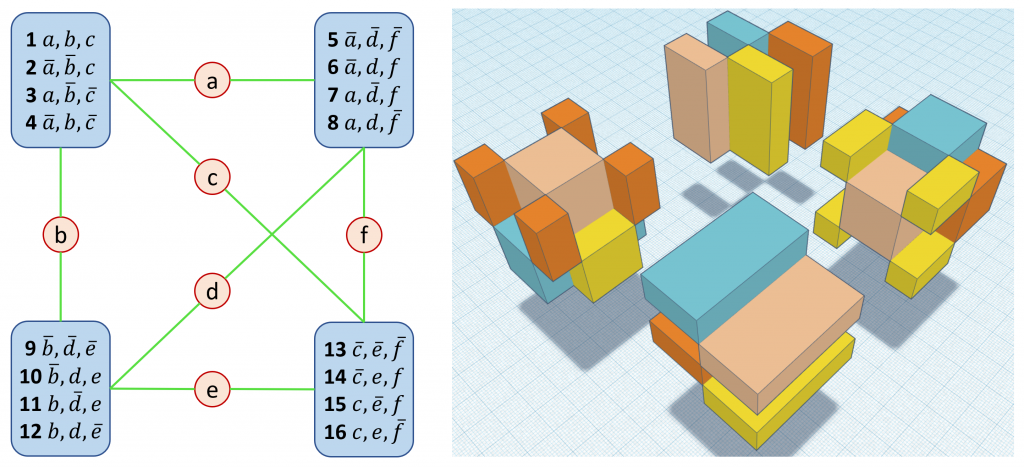
Cette représentation de SAT a un intérêt pédagogique. Elle permet de visualiser les déductions réalisables sur de petites formules et notamment un phénomène qui est lié au manque d’efficacité de la Résolution pour réfuter certaines formules, à savoir la nécessité de produire des dalles plus petites que les dalles initiales avant d’obtenir des dalles qui « s’agencent » suffisamment bien pour se recombiner en dalles de plus en plus grandes jusqu’à celle couvrant tout l’espace, c’est à dire la clause vide. Voici par exemple la représentation d’une formule à 6 variables où ce phénomène apparaît. L’hypercube de degré 6 est représenté par un tableau de Karnaugh en trois dimensions.

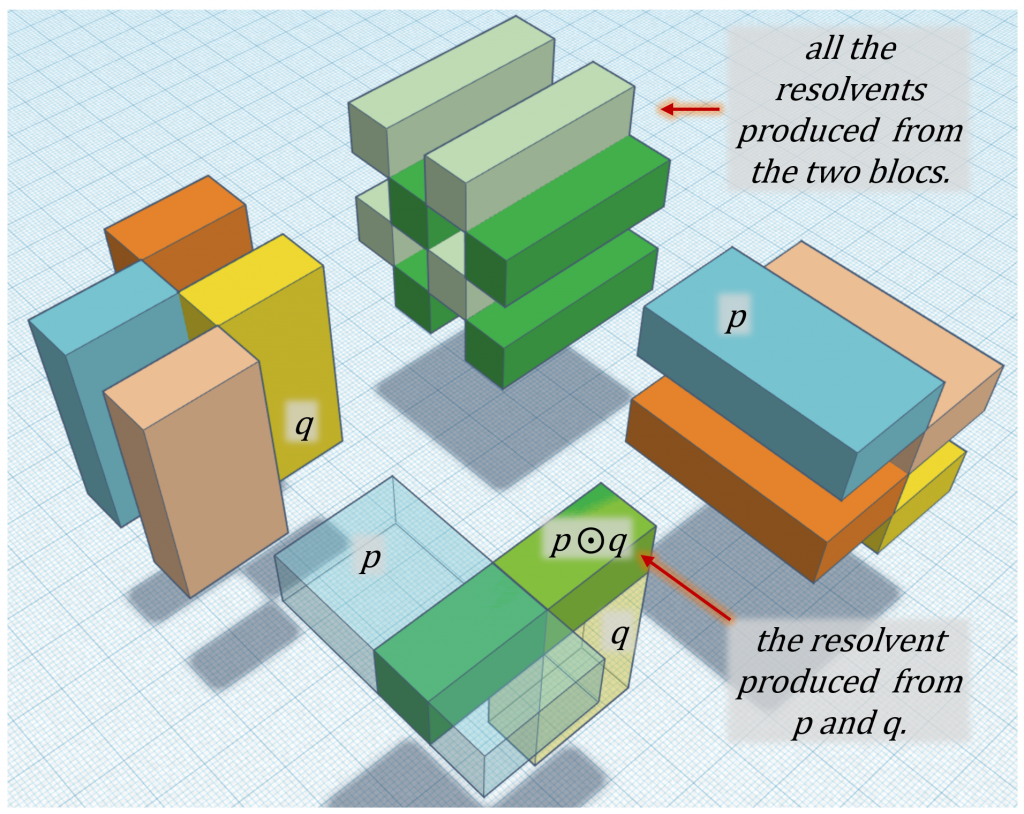
Les résolvantes pouvant être produites à partir de ces clauses sont toutes plus petites (en terme de volumes des dalles représentant ces clauses) que leurs prémisses. Voici une représentation de certaines d’entre elles.

Résoudre SAT par Résolution inversée

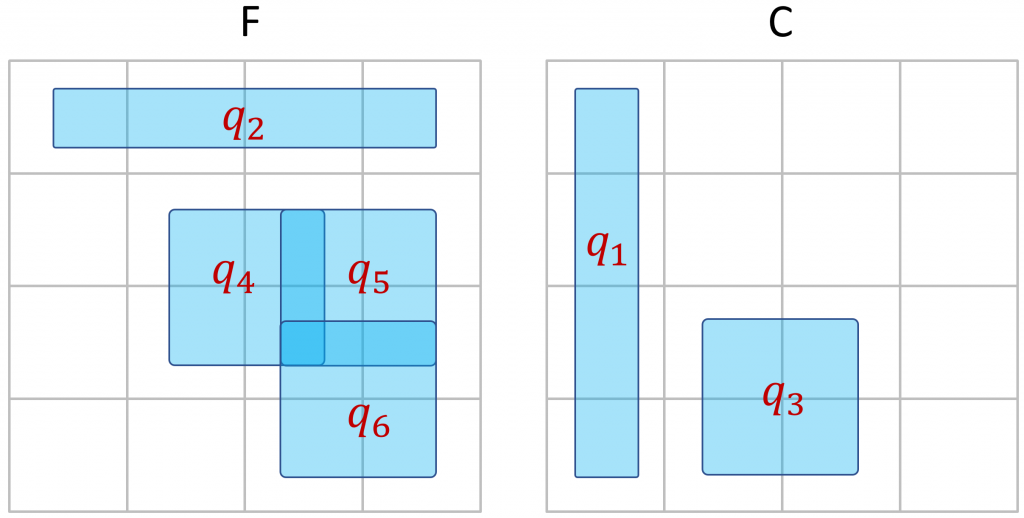
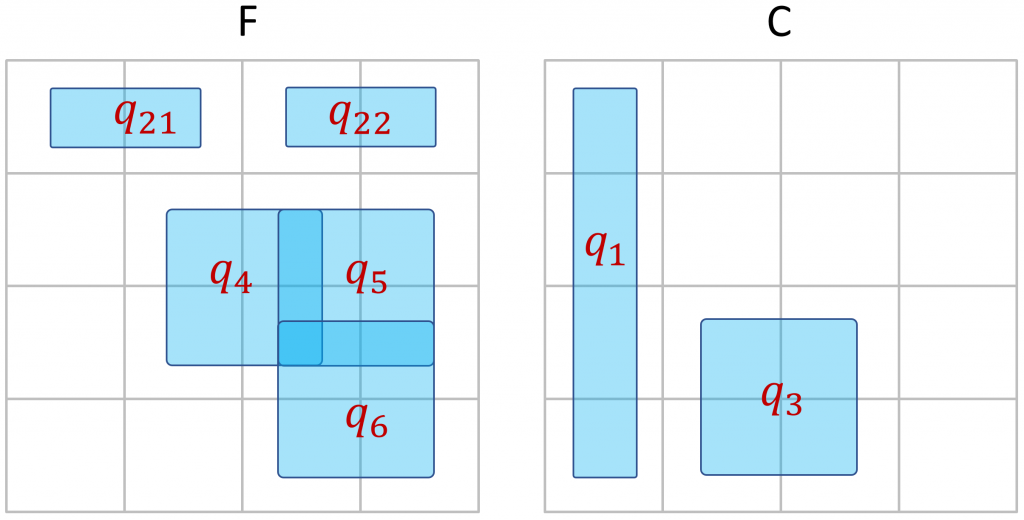
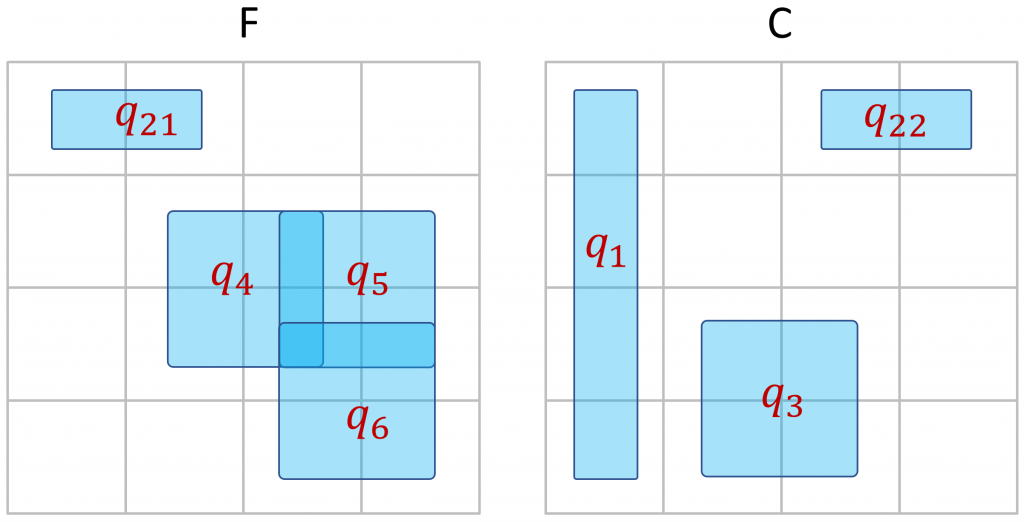
Mais au delà de l’intérêt pédagogique, cette représentation m’a inspiré l’idée d’un algorithme original (jusqu’à plus ample informé) pour résoudre SAT. Cet algorithme consiste à utiliser des clauses ou des morceaux de clauses de la formule à traiter pour tenter créer un pavage sans recouvrement d’un espace initialement vide. S’il ne reste plus de clause de la formule permettant de compléter le pavage sans recouvrement, alors on « casse » certaines clauses en deux à l’aide d’un opérateur qui pourrait être appelé déRésolution : on remplace une clause q, par deux clauses q \vee x et q \vee \neg x. Voici quelques étapes d’exécution de cet algorithme avec la formule \Sigma présentée plus haut.

…

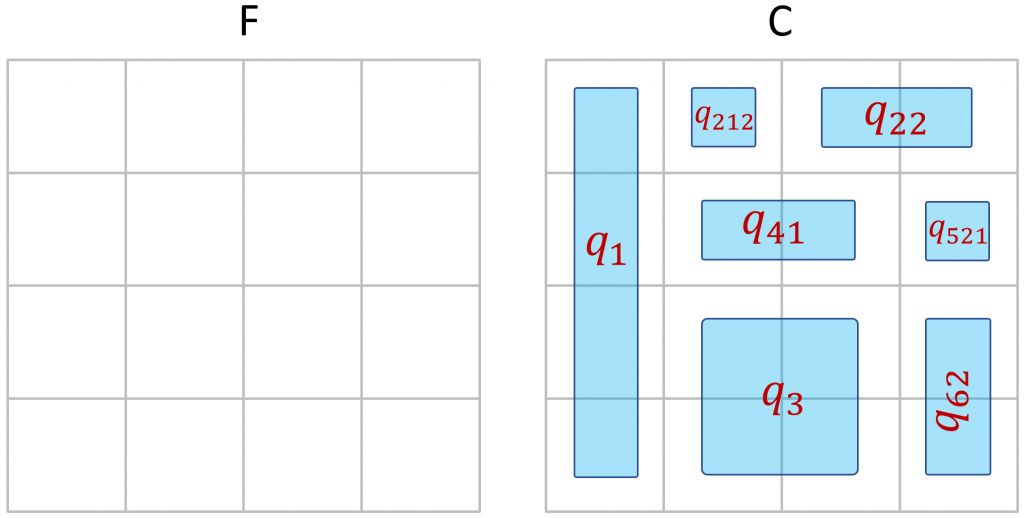
On peut s’attendre à ce que l’efficacité d’un tel algorithme, si applicable, soit largement dépendante de la manière de choisir les clauses à découper et la variable de « découpage » de ces clauses.

Nouvelles heuristiques pour solveurs SAT ?

L’idée de représenter la connaissance accumulée au cours de la résolution d’une instance SAT par un ensemble C de clauses ne se recouvrant pas, qui est la base de l’algorithme présenté précédemment, pourrait être exploitée par d’autres systèmes déductifs. Les déductions produites par des solveurs SAT de type CDCL ou DPLL avec redémarrages pourraient être guidées de manière à tenter de produire des clauses qui ne se recouvrent pas avec celles déjà ajoutées à l’ensemble C. La somme des volumes des dalles représentant les clauses de cet ensemble serait alors utilisé comme indicateur de progression de la recherche.