Je présente dans ce billet une idée qui est décrite en anglais dans cette note. Elle consiste à exploiter des séquences d’hypothèses et de déductions pour produire des clauses qui sont conséquences logiques de celles ayant servi à réaliser les déductions, comme le font les solveurs CDCL, mais avec une approche différente, permettant de produire d’autres clauses.
Par exemple, considérons cette séquence contradictoire d’hypothèses et de déductions qui pourrait être produite par un solveur SAT de type CDCL ou même DPLL. Je propose d’appeler une telle séquence AUP-séquence contradictoire (AUP pour Assumption and Unitary Propagation).
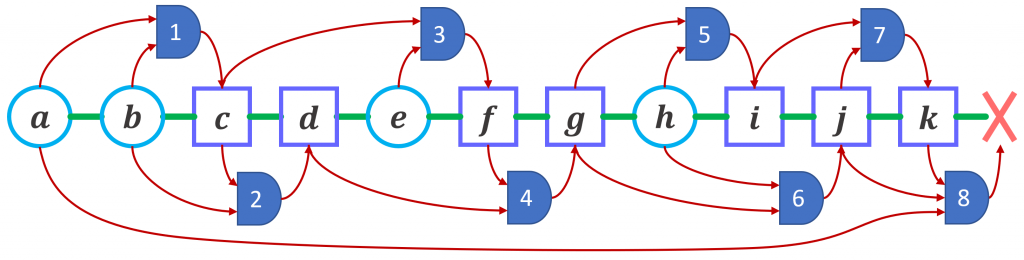
Un solveur de type CDCL analyse une telle séquence de bas en haut, en partant de la clause ayant provoqué le conflit et en remontant les déductions dans l’ordre chronologique inverse. A chaque étape de cette analyse, on obtient un UP-nogood, c’est à dire un ensemble de littéraux permettant à la propagation unitaire de produire la clause vide. Voici les nogoods pouvant être produits de cette manière. Le quatrième noggod est celui généralement exploité par les solveurs CDCL avec schéma d’apprentissage « first UIP ».
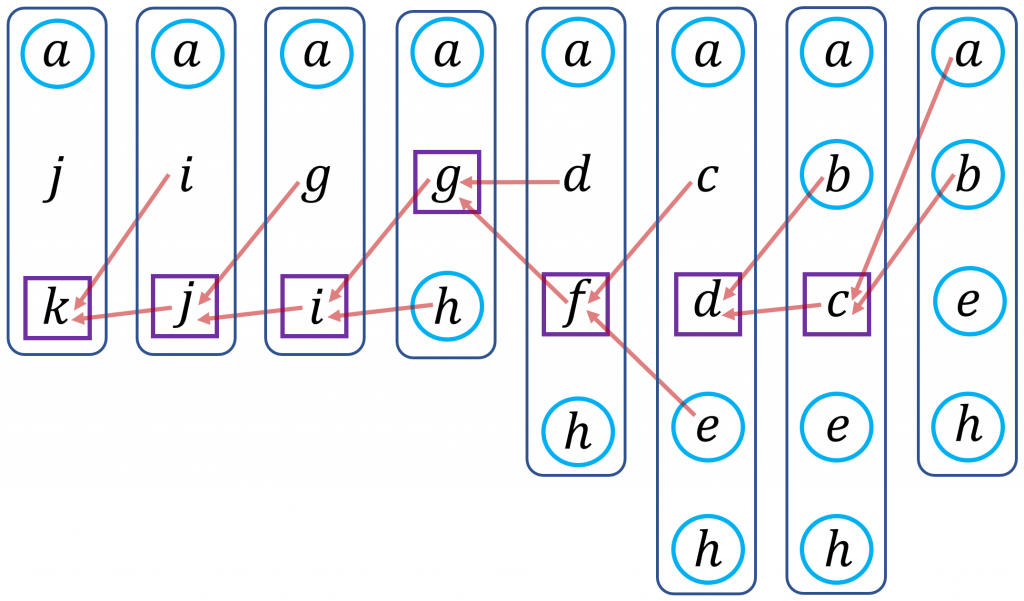
L’idée que je propose consiste à produire des nogoods en exploitant les hypothèses et certaines des déduction par une analyse descendante d’une AUP-séquence. Avec la même séquence d’exemple, voici les nogoods pouvant être produits.
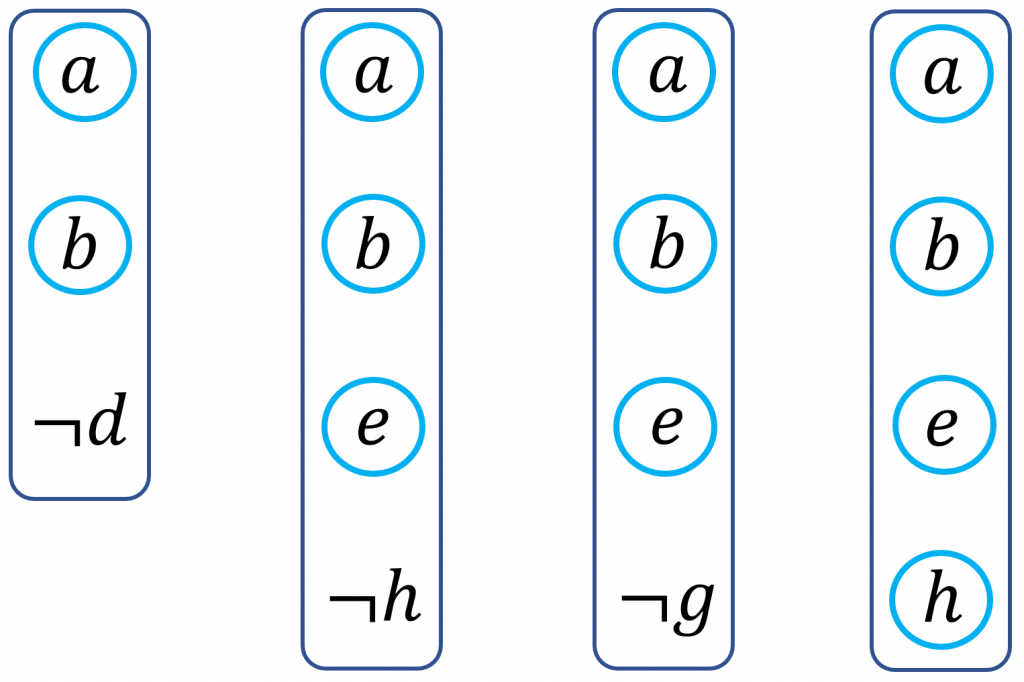
Le principe est simple. Considérons par exemple le troisième nogood. Il résulte du fait que les hypothèses a, b et e permettent à la propagation unitaire de déduire le littéral g. En conséquence, {a, b, e, ¬g} est un UP-nogood et sa négation, la clause (¬a ∨ ¬b ∨ ¬e ∨ g) , est une conséquence logique des clauses ayant permis la déduction de g.
Ce principe de déduction a la puissance d’expression de la Résolution et est donc tout à fait crédible comme base pour la conception de solveurs SAT. De plus, il a l’avantage de permettre de réaliser des déductions à partir de AUP-séquences qui ne sont pas contradictoires ou qui n’ont pas été développées jusqu’à produire une contradiction (sauf bien sûr pour le dernier nogood qui est la négation des hypothèses et qui n’est valable que si ces hypothèses produisent une contradiction).